|
|
…Όμως εμείς δεν είχαμε, ότι κομμένα τα γιοφύρια πίσω μας…
Οδυσσέας Ελύτης, Άξιον Εστί
|
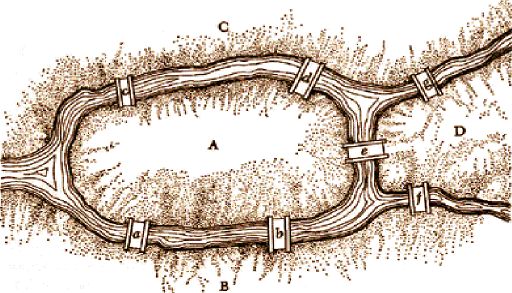
Τοπογραφικό διάγραμμα των επτά γεφυρών του Κένιγκσμπεργκ, που χωρίζει την πεδιάδα σε τέσσερις περιοχές: τις δύο όχθες B και C και τα δύο νησιά A και D
|
Ένα από τα προσφιλέστερα θέματα των πολιτικών στις προεκλογικές περιόδους
είναι οι γέφυρες. «Θα σας κάνω και γεφύρια», υποσχόταν ο πολιτευτής του
ανεκδότου στους δυνάμει ψηφοφόρους του. «Μα δεν έχουμε ποτάμια», αντέτεινε ο
ανυποψίαστος κάτοικος της Κάτω Ραχούλας. «Θα σας κάνω και ποτάμια», τον
αποστόμωνε ψύχραιμα ο αιώνιος κύριος Θα.
Βρισκόμαστε εν μέσω μιας παρατεταμένης προεκλογικής – προολυμπιακής περιόδου
και οι γέφυρες είναι και πάλι ψηλά στην ημερήσια διάταξη. Οι προτιμήσεις
ποικίλλουν: γέφυρες στρωμένες με πίσσα και δάφνες στους δρόμους που οδηγούν
στα στάδια, για να περάσουν ανεμπόδιστα τα τελευταίας βιοτεχνολογίας
αναβολικά, διακριτικά κρυμμένα μέσα στα πολύπαθα κορμιά των αθλητών. Γέφυρες
από πλαστελίνη και αφρολέξ, για να σαρκάζει η αντιπολίτευση διαπιστώνοντας ότι
«μακέτες ήταν και μακέτες παραμένουν». Ημιτελή γιοφύρια made in Arta για να τα
εγκαινιάζει η κυβέρνηση και να υπερηφανεύεται ότι «έξι μήνες μπρος, δύο χρόνια
πίσω, πέντε δισ. πάνω, ένα δισ. κάτω, εμείς παράγουμε έργο». Οι Αμερικανοί
πάλι προτιμούν τις γέφυρες του Δούναβη και των παραποτάμων του. «Όπως και να
το κάνεις, βρε παιδί μου, δίνουν καλύτερο στόχο από το αεροπλάνο, είναι πολύ
γκλάμορους να τις βομβαρδίζεις. Όπως… Βιετνάμ και καλύτερα», που θα ‘λεγε
και η διαφήμιση.
Το 1255, οι Ιππότες του Τευτονικού Τάγματος, επιστρέφοντας από τις
Σταυροφορίες, έχτισαν στα παράλια της Βαλτικής ένα φρούριο, γύρω από το οποίο
σταδιακά αναπτύχθηκε μια ολόκληρη πόλη. Το Κένιγκσμπεργκ – δηλαδή το «όρος του
βασιλιά» όπως ονομάστηκε – εξελίχθηκε σε σημαντικό εμπορικό, στρατιωτικό και
πολιτιστικό κέντρο, μέχρι που τον 15ο αιώνα έγινε πρωτεύουσα της Ανατολικής
Πρωσίας. Το Πανεπιστήμιό του ιδρύθηκε το 1544 από τον δούκα Αλβέρτο, και κατά
καιρούς φιλοξένησε κορυφαίους φυσικομαθηματικούς, όπως τον Μπεσέλ, τον
Τζακόμπι και τον Χέλμχολτζ. Το Κένιγκσμπεργκ είναι γενέτειρα πολλών
μαθηματικών, μεταξύ των οποίων ο Χίλμπερτ και ο Γκόλντμπαχ. Είναι ακόμα η
πατρίδα του μεγάλου Γερμανού φιλοσόφου Ιμάνουελ Καντ (1724-1804), που έζησε
εκεί το μεγαλύτερο μέρος της ζωής του. Την πόλη διασχίζει ο ποταμός Πρέγκελ,
που τα επτά γεφύρια του αποτέλεσαν αντικείμενο ενός προβλήματος το οποίο
ξεκίνησε ως τουριστική ατραξιόν και εξελίχθηκε σ’ έναν από τους πιο
σημαντικούς κλάδους των σύγχρονων Μαθηματικών.
|
Ο ποταμός Πρέγκελ με μερικές από τις γέφυρές του όπως είναι σήμερα
|
Το πρόβλημα που έπρεπε να λύσει ο περιηγητής, ήταν να επισκεφθεί και τα επτά
γεφύρια, διασχίζοντας το καθένα μία ακριβώς φορά. Ήταν ένα πρόβλημα
«μονοκοντυλιάς», σαν αυτά που και σήμερα προτείνουν στη στήλη ψυχαγωγίας τους
τα διάφορα έντυπα. Επί πολλά χρόνια, τουρίστες και ντόπιοι προσπαθούσαν μάταια
να λύσουν το πρόβλημα. Είτε, όταν ολοκλήρωναν την περιήγησή τους διαπίστωναν
ότι είχαν παραλείψει κάποια γέφυρα, είτε αναγκάζονταν να περάσουν από κάποια
γέφυρα δύο φορές.
Κάποτε ενδιαφέρθηκε για το πρόβλημα και ο μεγάλος Ελβετός μαθηματικός
Leonhard Euler (1707-1783). H ιστορία δεν αναφέρει αν ο Euler πέρασε αμέτρητες
ώρες τσαλακώνοντας και σκίζοντας το ένα μετά το άλλο αντίγραφα του χάρτη του
Κένιγκσμπεργκ, στην προσπάθειά του να λύσει το πρόβλημα στα χαρτιά ή αν
έλειωσε τα παπούτσια του περιδιαβάζοντας τους δρόμους της πόλης και μελετώντας
το θέμα επιτόπου. Το μόνο που γνωρίζουμε, είναι πως ύστερα από λίγο διατύπωσε
ένα πολύ πιο γενικό πρόβλημα, μαζί με τη λύση του: «Με δεδομένο ένα
οποιοδήποτε σύστημα διακλαδώσεων ενός ποταμού, που να χωρίζει με οποιονδήποτε
τρόπο μια πεδιάδα σε περιοχές και για οποιονδήποτε αριθμό γεφυριών που
συνδέουν μεταξύ τους αυτές τις περιοχές, να ελεγχθεί αν είναι εφικτή μια
διαδρομή που να διέρχεται από κάθε γέφυρα μία ακριβώς φορά». Παρατήρησε ότι το
συγκεκριμένο πρόβλημα θα μπορούσε να λυθεί με αναλυτική απαρίθμηση όλων των
δυνατών διαδρομών και έλεγχο για το αν κάποια απ’ αυτές πληροί τις
προδιαγραφές της «μονοκοντυλιάς». Κάτι τέτοιο όμως θα ήταν και εξαιρετικά
επίπονο, λόγω του μεγάλου αριθμού των συνδυασμών, και «χαμένος κόπος», αφού σε
κάθε νέα περίπτωση η προηγούμενη ανάλυση θα ήταν άχρηστη. Αντίθετα, ο Euler
έλυσε το πρόβλημα θεωρητικά, διατυπώνοντας ένα αριθμητικό κριτήριο που ανάλογα
με το πλήθος των περιοχών και των γεφυρών που τις συνδέουν επιτρέπει να
αποφανθούμε αν η μονοκοντυλιά είναι εφικτή ή όχι.
H θεωρία των γραφημάτων
|
Ο Ελβετός μαθηματικός Leonhard Euler που έλυσε το πρόβλημα του Κένιγκσμπεργκ βάζοντας τις βάσεις για τη σύγχρονη μαθηματική θεωρία των γραφημάτων
|
H μέθοδος του Euler σηματοδότησε τη γέννηση ενός νέου κλάδου των Μαθηματικών,
της θεωρίας των γραφημάτων. Σήμερα η θεωρία των γραφημάτων έχει πληθώρα
εφαρμογών, ξεκινώντας από τα δίκτυα υδροδότησης, ηλεκτροδότησης και
αποχέτευσης, τα δίκτυα διανομής και διακίνησης προϊόντων και φτάνοντας μέχρι
τον στρατιωτικό αμυντικό σχεδιασμό μιας χώρας.
Μετά τον B’ Παγκόσμιο Πόλεμο το Κένιγκσμπεργκ περιήλθε, με τη Συνθήκη του
Πότσνταμ, στη Σοβιετική Ένωση, και μετονομάστηκε σε Καλίνινγκραντ. Με την
κατάρρευση της Σοβιετικής Ένωσης, το 1991, το Καλίνινγκραντ περιήλθε στη
Ρωσία, δημιουργώντας ένα ακόμα άλυτο πολιτικομαθηματικό πρόβλημα, που κι αυτό
εντάσσεται στη θεωρία των γραφημάτων. Πράγματι, ανάμεσα στο Καλίνινγκραντ και
την υπόλοιπη Ρωσία παρεμβάλλονται οι τρεις Δημοκρατίες της Βαλτικής. Δεν
υπάρχει λοιπόν τρόπος να μεταβεί κανείς οδικώς από το ένα τμήμα της Ρωσίας στο
άλλο, παραμένοντας στο εσωτερικό της χώρας. Οι συνθήκες που επιτρέπουν την
ελεύθερη διακίνηση των πολιτών διά μέσου των Βαλτικών Χωρών τίθενται σε
αμφισβήτηση, από τη στιγμή που οι χώρες αυτές θα ενταχθούν στην Ευρωπαϊκή
Ένωση και θα κυρώσουν τη Συνθήκη του Σέγκεν.
Όμως, αυτό το πρόβλημα ανήκει αποκλειστικά στη δικαιοδοσία των πολιτικών.
Συνεπώς, η όποια λύση δοθεί, αν ποτέ δοθεί, δεν θα παρέχει καμιά εγγύηση ούτε
ως προς τη σταθερότητά της ούτε ως προς την αδιαμφισβήτητη και ομόφωνη αποδοχή της.
INFO
Για περισσότερα προτείνουμε το κεφάλαιο 5 του βιβλίου του C.L. Liu, Στοιχεία
διακριτών Μαθηματικών. Το κεφάλαιο διαβάζεται σχεδόν ανεξάρτητα από το
υπόλοιπο βιβλίο και περιλαμβάνει (§ 5.6) μια πλήρη παρουσίαση της μεθόδου του
Euler. Απαιτεί, ωστόσο, μια εξοικείωση με τη μαθηματική ορολογία. Για μια πιο
«light» προσέγγιση, συμβουλευθείτε τον δικτυακό τόπο http: //www.mathforum.org/isaac/mathhist.html.
Ο Τεύκρος Μιχαηλίδης είναι διδάκτωρ των Μαθηματικών. Εργάζεται ως
καθηγητής στη Μέση Εκπαίδευση και ως μεταφραστής.