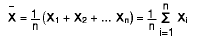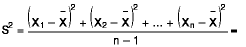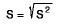ANOIXTO MBA H περιγραφή των Mεταβλητών

Όταν ασχολούμαστε με την περιγραφή κατηγορικών μεταβλητών, ο πίνακας

συχνοτήτων μάς δίνει σχεδόν όλη την πληροφορία που χρειαζόμαστε. Αν θέλουμε να

περιορίσουμε την περιγραφή μας σε ένα περιληπτικό μέτρο, μπορούμε να

αναφέρουμε την κατηγορία με τη μεγαλύτερη συχνότητα (επικρατούσα

κατηγορία).

Αντίθετα στις ποσοτικές, τα πράγματα είναι πιο σύνθετα. Ακόμα κι αν

κατασκευάσουμε τον πίνακα συχνοτήτων με κάποια ομαδοποίηση της αρχικής μας

μεταβλητής, αυτό δεν είναι αρκετό για να πάρουμε μια συνολική ιδέα της

συμπεριφοράς της. Έτσι, σε αυτή την περίπτωση μπορούμε να υπολογίσουμε

διάφορους δείκτες που μετρούν διαφορετικά χαρακτηριστικά των τιμών που

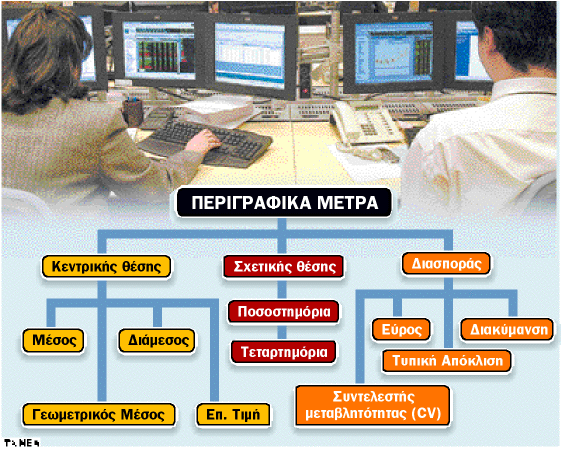
παρατηρούμε. Αυτοί οι δείκτες χωρίζονται σε τέσσερις μεγάλες κατηγορίες:

1. Μέτρα κεντρικής θέσης ή τάσης

2. Μέτρα διασποράς ή διακύμανσης των τιμών

3. Μέτρα σχετικής θέσης

4. Μέτρα σχήματος

METPA ΚΕΝΤΡΙΚΗΣ ΘΕΣΗΣ

Ας δούμε πρώτα τα μέτρα κεντρικής θέσης, τα οποία μετρούν το «κέντρο» των

τιμών. Μπορούμε να τα σκεφτούμε ως τιμές που αντιπροσωπεύουν ένα μέσο ή

συνηθισμένο άτομο στο δείγμα μας. Πιο γνωστά μέτρα είναι η μέση τιμή

και η διάμεσος. H μέση τιμή είναι το άθροισμα όλων των τιμών

διαιρεμένο με τον συνολικό αριθμό των ατόμων που εξετάζουμε. Ανάλογα με το πού

αναφερόμαστε (στον πληθυσμό ή στο δείγμα) έχουμε την πληθυσμιακή μέση τιμή

(μ) και τη δειγματική μέση τιμή (). H δειγματική μέση τιμή

(ή απλά δειγματικός μέσος) δίνεται από τον τύπο:

όπου Xi είναι η τιμής της μεταβλητής για το i άτομο και n

είναι ο συνολικός αριθμός ατόμων στο δείγμα (μέγεθος δείγματος). Δηλαδή, μας

δίνει την τιμή που θα έπρεπε να πάρει η μεταβλητή αν το συνολικό άθροισμα

μοιραστεί ίσα σε όλα τα άτομα του δείγματος. Ένα παράδειγμα: Σε μια εταιρεία

καταγράφουμε τους μηνιαίους μισθούς των εργαζομένων. Το άθροισμά τους δίνει το

ποσό που διαθέτει η εταιρεία μηνιαίως για μισθούς. Αν η εταιρεία αποφασίσει να

συνεχίσει να δίνει συνολικά το ίδιο ποσό χρημάτων για μισθούς αλλά υιοθετήσει

την πολιτική όλοι οι υπάλληλοι να έχουν τον ίδιο μισθό, αυτός θα είναι ίσος με

τη μέση τιμή. Παρ’ όλο που ο μέσος είναι πολύ δημοφιλής, έχει κάποια

μειονεκτήματα. Το κύριο μειονέκτημα είναι ότι επηρεάζεται από ακραίες τιμές.

Έτσι, αν θέλουμε να χρησιμοποιήσουμε το μέσο εισόδημα ως δείκτη ευημερίας των

πολιτών ενός κράτους, αυτό θα παρουσιάζεται αυξημένο από την παρουσία λίγων

και μόνο ευκατάστατων πολιτών, με συνέπεια να μην έχουμε την πραγματική

εικόνα.

Αντίθετα, η διάμεσος είναι η τιμή που χωρίζει το δείγμα στη μέση,

δηλαδή περίπου 50% των ατόμων έχουν μικρότερες τιμές από τη διάμεσο (και το

άλλο 50% μεγαλύτερες τιμές). H διάμεσος δεν επηρεάζεται από ακραίες τιμές.

Έτσι, σε μία χώρα που το 90% των πολιτών έχει χαμηλό εισόδημα ενώ το 10% πολύ

υψηλό, η διάμεσος θα μας δώσει μια αντικειμενική εικόνα της πραγματικότητας

(δηλαδή μια χαμηλή τιμή).

METPA ΔΙΑΣΠΟΡΑΣ

Τα μέτρα διασποράς εκτιμούν πόσο απλωμένες είναι οι τιμές της

μεταβλητής που εξετάζουμε. Πιο γνωστό μέτρο διασποράς είναι η

διακύμανση. H διακύμανση, ανάλογα με το πού αναφέρεται, διακρίνεται σε

πληθυσμιακή (σ2) και σε δειγματική διακύμανση (S2). H δειγματική

διακύμανση δίνεται από τον τύπο

Στην ουσία, είναι η μέση τετραγωνική απόσταση τής κάθε τιμής από τον

δειγματικό μέσο. Επειδή οι μονάδες μέτρησης της διακύμανσης είναι ίσες με το

τετράγωνο των μονάδων μέτρησης της αρχικής μας μεταβλητής (π.χ. αν X μετράει

ύψος σε μέτρα, η διακύμανση θα δίνεται σε τετραγωνικά μέτρα), χρησιμοποιούμε

την τυπική απόκλιση, η οποία δεν είναι τίποτα άλλο από τη τετραγωνική ρίζα της

διακύμανσης. Δηλαδή:

METPA ΣΧετικησ θεσησ

Τα μέτρα σχετικής θέσης επικεντρώνονται όχι στο κέντρο των τιμών, αλλά σε

άλλες θέσεις της κατανομής τους. Για παράδειγμα, το Τμήμα Διοίκησης Προσωπικού

μπορεί να ενδιαφέρεται να εντοπίσει το 10% των υπαλλήλων με τις υψηλότερες

πωλήσεις, ώστε να τους προωθήσει σε πιο υψηλές θέσεις. Τα πιο γνωστά μέτρα

σχετικής θέσης είναι το πρώτο και το τρίτο τεταρτημόριο (Q1 και Q3), τα οποία

χωρίζουν τις τιμές σε 25% – 75% και 75% – 25% αντίστοιχα.

METPA ΣΧΗΜΑΤΟΣ

Τέλος, στα μέτρα σχήματος έχουμε τους δείκτες συμμετρίας και

κυρτότητας. Ο πρώτος μετράει τη συμμετρικότητα της κατανομής των τιμών,

ενώ ο δεύτερος την οξύτητα της κορυφής τής κατανομής.

Tips

H μέση…

…τιμή είναι το άθροισμα όλων των τιμών διαιρεμένο με τον συνολικό αριθμό

των ατόμων που εξετάζουμε

Ενδεικτική βιβλιογραφία

1. Berenson, Μ.L., Levine, D.Μ. και Krehbiel, Τ.Κ. (2002). Basic

Business Statistics. Prentice Hall.

2. L.J. Kazmier (1995). Business Statistics. Schaum’s Outlines.

3. Τσάντας, Μωυσιάδης, Μπαγιάτης, Χατζηπαντελής (1999). Ανάλυση

Δεδομένων με τη βοήθεια στατιστικών πακέτων. Εκδόσεις Ζήτη.

4. Chatterjee S., Handcock Μ.S. and Simonoff J.S. (1995), A Casebook

for a First Cause in Statistics and Data Analysis, John Wiley and Sons.

5. Gonick, L. και Smith, W. (1994). The Cartoon Guide to Statistics.