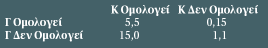|
|
|
|
H ιδέα ότι τα παιχνίδια αντικατοπτρίζουν τις ανθρώπινες συγκρούσεις και
συνδιαλλαγές είναι παμπάλαια. H Θεωρία των Παιγνίων ασχολείται με τις
αποφάσεις δύο ή περισσοτέρων ατόμων με διαφορετικούς σκοπούς και στόχους, υπό
συνθήκες αβεβαιότητας, όπου κάθε άτομο (παίκτης) προσπαθεί να
βελτιστοποιήσει τη δική του απόφαση, εις βάρος των άλλων ή σε συνεργασία με
τους άλλους, με βάση τη διαμόρφωση συνασπισμών.
ΒΑΣΙΚΕΣ ΥΠΟΘΕΣΕΙΣ
* Ορθολογικότητα: H δράση που αναλαμβάνει κάθε παίκτης είναι η
καλύτερη δυνατή γι’ αυτόν. Μεγιστοποιεί τα κέρδη και ελαχιστοποιεί τις ζημιές.
* Τέλεια Πληροφόρηση: Σε κάθε στάδιο του παιχνιδιού ο παίκτης
ξέρει όλες τις προηγούμενες κινήσεις, τόσο τις δικές του όσο και των άλλων,
καθώς και όλες τις επιτρεπόμενες μελλοντικές επιλογές.
Τα Πειραματικά Οικονομικά (Experimental Economics) εξετάζουν την εγκυρότητα
αυτών των υποθέσεων ερευνώντας πώς συμπεριφέρονται οι άνθρωποι σε ελεγχόμενο
περιβάλλον.
ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ
Τα παίγνια χαρακτηρίζονται από:
* Παίκτες: Είναι οι αντίπαλοι (άνθρωποι ή οργανισμοί που
αποφασίζουν).
* Κανόνες: Ορίζουν ποιος μπορεί να κάνει τι και πότε.
* Ανταμοιβές: Οι δυνατές εκβάσεις του παιγνίου, τα κέρδη ή οι
απώλειες που απορρέουν από τις επιλογές των παικτών, σε αριθμούς.
* Στρατηγικές: Σχέδια δράσης για κάθε δυνατή περίπτωση του
παιγνίου.
* Ισορροπία: Ένα σταθερό αποτέλεσμα. Ένα σύνολο στρατηγικών, μία
για κάθε παίκτη, είναι σε ισορροπία, όταν ουδείς παίκτης μπορεί να αλλάξει
μονομερώς τη στρατηγική του για να πετύχει καλύτερη ανταμοιβή.
ΤΑΞΙΝΟΜΗΣΗ
Τα παίγνια ταξινομούνται με βάση:
*Τον αριθμό των παικτών
*Τους κανόνες
* Τη διαμόρφωση ή όχι συνασπισμών και συνεργασιών
* Τη σειρά λήψης αποφάσεων
* Τον αριθμό των στρατηγικών
* Την τύχη
* Την πληροφόρηση
* Τις ανταμοιβές
Παίγνια μηδενικού αθροίσματος: Το κέρδος τού ενός είναι ίσο και
προέρχεται από τη ζημιά του άλλου, με συνέπεια το άθροισμα των ανταμοιβών να
είναι μηδέν.
Παίγνια γενικού μη μηδενικού αθροίσματος: Οι παίκτες μπορεί να
κερδίσουν ή να χάσουν και οι δύο με βάση τη στρατηγική τους.
Στη σύγχρονη οικονομική θεωρία υπάρχει έντονη αντιπαράθεση σχετικά με το αν η
οικονομία στο σύνολό της είναι παίγνιο μηδενικού αθροίσματος ή όχι. Αν ναι,
τότε όλη η οικονομία είναι μια συνεχής ανακατανομή του ίδιου πλούτου. Καθώς οι
πλούσιοι γίνονται πλουσιότεροι, οι φτωχοί γίνονται φτωχότεροι. Για τους
περισσότερους οικονομολόγους, όμως, δεν πρόκειται περί παιγνίου μη μηδενικού
αθροίσματος. Καθώς δημιουργείται πλούτος, οι πλούσιοι γίνονται πλουσιότεροι,
αλλά και οι φτωχοί γίνονται πλουσιότεροι.
H πιο συνήθης περιγραφή ενός παιγνίου γίνεται με τη βοήθεια ενός πίνακα ή
μήτρας γραμμών και στηλών, που περιέχει όλες τις δυνατές στρατηγικές κάθε
παίκτη, καθώς και τα αποτελέσματα που προκύπτουν από κάθε συνδυασμό
στρατηγικών. Σε κάθε γραμμή του πίνακα υπάρχει η στρατηγική του παίκτη 1 και
σε κάθε του στήλη η στρατηγική του παίκτη 2. Σε κάθε κελί του πίνακα υπάρχει
ένα ζεύγος αριθμών (χ, ψ), όπου το χ αντιπροσωπεύει τις ανταμοιβές του παίκτη
1 και το ψ τις ανταμοιβές του παίκτη 2 (βλ. Γράφημα 1).
Σε ένα παίγνιο που παρουσιάζεται σε μορφή πίνακα εμφανίζονται οι στρατηγικές
των παικτών, καθώς και τα αποτελέσματα που πετυχαίνουν, δεν εμφανίζονται
στοιχεία όπως η χρονική στιγμή των αποφάσεων, το ποιος είναι πρώτος και ποιος
δεύτερος χρονικά, το αν παίζουν μαζί κ.ά. Αυτές οι λεπτομέρειες της
αλληλεπίδρασης των παικτών εμφανίζονται όταν το παίγνιο παρουσιάζεται με μορφή
δένδρου.
KYPIAPXIA ΣΤΡΑΤΗΓΙΚΩΝ
Μια στρατηγική A κυριαρχεί έναντι μιας στρατηγικής B, αν για όλους τους
συνδυασμούς στρατηγικών των άλλων παικτών η στρατηγική A έχει μεγαλύτερες
ανταμοιβές σε σχέση με τη B. H B, τότε, χαρακτηρίζεται ως Κυριαρχούμενη
Στρατηγική. Αν η στρατηγική A κυριαρχεί έναντι όλων των εναλλακτικών
στρατηγικών ενός παίκτη λέγεται Κυρίαρχη Στρατηγική για τον παίκτη αυτόν.
ΘΕΩΡΗΜΑΤΑ
Τα Θεωρήματα της Θεωρίας των Παιγνίων:
* Θεώρημα MINIMAX: Σύμφωνα με το θεώρημα αυτό, υπάρχει ένα σημείο
ισορροπίας, ένα σύνολο βέλτιστων στρατηγικών για κάθε παίκτη, το σημείο
MINIMAX, στο οποίο η μεγιστοποίηση του ελάχιστου κέρδους είναι ίση με την
ελαχιστοποίηση της μέγιστης ζημίας.
Το θεώρημα αυτό εκφράζει την ορθολογική δράση κατά τον von Neumann, ο οποίος
πίστευε ότι «χωρίς αυτό δεν θα μπορούσε να υπάρχει Θεωρία των Παιγνίων». Το
θεώρημα αυτό ουσιαστικά διατυπώνει μαθηματικά το ρητό «να ελπίζεις για το
καλύτερο και να προετοιμάζεσαι για το χειρότερο».
Το θεώρημα αυτό λέει: Για κάθε παίγνιο δύο ατόμων μηδενικού αθροίσματος
υπάρχει μια μεικτή στρατηγική για κάθε παίκτη, τέτοια ώστε η αναμενόμενη
ανταμοιβή και για τους δύο είναι η ίδια τιμή T όταν οι παίκτες επιλέγουν αυτές
τις στρατηγικές. Επιπλέον, η T είναι η βέλτιστη ανταμοιβή που μπορεί να
αναμένει κανείς παίζοντας το παιχνίδι. Άρα, αυτές οι μεικτές στρατηγικές είναι
οι βέλτιστες στρατηγικές που μπορούν να επιλέξουν οι δύο παίκτες.
* Θεώρημα ισορροπίας του Nash (γενίκευση του θεωρήματος MINIMAX): Κάθε
παίγνιο ν-προσώπων άνευ συνεργασίας (μηδενικού αθροίσματος ή όχι), για το
οποίο κάθε παίκτης διαθέτει ένα σύνολο καθαρών στρατηγικών, έχει τουλάχιστον
ένα σύνολο ισορροπίας των στρατηγικών. Με απλά λόγια, η ισορροπία κατά Nash
(την ιστορία του οποίου είδαμε πρόσφατα στην ταινία «Ένας υπέροχος άνθρωπος»)
σε ένα παίγνιο είναι μια κατάσταση από την οποία δεν συμφέρει κανέναν παίκτη
να ξεφύγει μεμονωμένα. (Για περισσότερες πληροφορίες βλέπε «Θεωρία των
Παιγνίων, Αφιέρωμα στον John Nash, Οι εργασίες του στη Θεωρία Παιγνίων και οι
επαναστατικές εφαρμογές τους στις κοινωνικές και φυσικές επιστήμες», Συλλογικό
Έργο, Εκδόσεις Ευρασία, 2002).
Το δίλημμα των φυλακισμένων
Δύο ύποπτοι για ληστεία, οι Γ και K, κρατούνται για διακίνηση ναρκωτικών. Ο
ανακριτής μιλάει και στους δύο ξεχωριστά και προσπαθεί να τους πείσει να
ομολογήσουν. Τα ενδεχόμενα που υπάρχουν είναι:
1. Να ομολογήσουν και οι δύο, οπότε θα μείνουν στη φυλακή 5 χρόνια.
2. Να μην ομολογήσει κανείς, οπότε θα μείνουν στη φυλακή έναν χρόνο για
τη διακίνηση.
3. Να ομολογήσει μόνο ο Γ, οπότε θα βγει από τη φυλακή, ενώ ο K θα
μείνει μέσα 15 χρόνια.
4. Να ομολογήσει μόνο ο K, οπότε θα βγει από τη φυλακή και ο Γ θα
μείνει μέσα15 χρόνια.
Τι πρέπει να κάνουν;
Το δίλημμα των φυλακισμένων είναι παίγνιο μη μηδενικού αθροίσματος. Ο πίνακας
του διλήμματος είναι:
|
|
Γενικά, μπορούμε να πούμε ότι το συμφέρον και των δύο είναι να μην
ομολογήσουν. Αν, όμως, ο Γ πιστεύει ότι ο K δεν θα ομολογήσει, τότε τον Γ τον
συμφέρει να ομολογήσει. Το ίδιο ισχύει αντίστοιχα και για τον K. Γενικά, για
κάθε επιλογή του K, τον Γ τον συμφέρει να ομολογήσει. Το ίδιο συμβαίνει και με
τον K. Τελικά ομολογούν και οι δύο.
Το παίγνιο αυτό έχει άμεση εφαρμογή στις διαφημίσεις. Αν και φαίνεται ότι οι
διαφημίσεις των εταιρειών «ισοφαρίζουν» η μία την άλλη και πως οι εταιρείες θα
κέρδιζαν αν καμία δεν έκανε διαφήμιση, όλες οι εταιρείες διαφημίζονται.
Επίσης, το πρόβλημα αυτό έχει μια σαφή ηθική διάσταση και στον πυρήνα του
βρίσκεται η σύγκρουση μεταξύ των ατομικών επιδιώξεων του καθενός και του
κοινού καλού.
|
|
* Τυχαίος έλεγχος για αναβολικά. Κάθε αθλητής πρέπει να αποφασίσει αν θα τα
χρησιμοποιήσει (αυξάνοντας τις πιθανότητες για διάκριση και διακινδυνεύοντας
να αποκαλυφθεί) ή όχι (μειώνοντας τις πιθανότητες διάκρισης, αν οι άλλοι που
τα χρησιμοποιούν δεν αποκαλυφθούν).
* Επένδυση για Έρευνα και Ανάπτυξη. Οι εταιρείες που επενδύουν για ανάπτυξη
ενός νέου προϊόντος, θα πρέπει να λάβουν υπόψη τους τις αντίστοιχες αποφάσεις
των ανταγωνιστών τους.
* Δημοπρασίες. H Θεωρία Παιγνίων μπορεί να χρησιμοποιηθεί στην ανάλυση των
στρατηγικών των δημοπρασιών. Οι δημοπρασίες είναι χρήσιμοι μηχανισμοί
προσδιορισμού τιμών.
Tips
Στα Παίγνια…
…γενικού μη μηδενικού αθροίσματος, οι παίκτες μπορεί να κερδίσουν ή να
χάσουν και οι δύο με βάση τη στρατηγική τους